3-Phased System

The phases are denoted by $\text{R},\text{Y},\text{B}$ in that order. $$

Why 3-phase?

Why not 1-phase?

• The current can be distributed into 3 wires instead of just 1.
  There is a maximum limit of how much current a wire can carry.
• Economical as less amount of wires.
  3-phase system requires $4$ wires ($3$ if balanced) while single phase system requires $6$.

Why not 2 or 4 or 6?

• Generators are volume constrained.
  3-phase system has the most optimum volume utilization in a generator.
• 3-wired 3-phase system carry 3 times the power of a 2-wired 1-phase system.
• As number of phases increases, the power advantage diminishes.
• As number of phases increases, the complexity of construction and maintanance increases.
• 3-phase motors have the most optimum volume utilization for a given output.

Balanced 3-phase

A 3-phase system is said to be balanced iff:

• Supply is balanced
• Loads are the same in each phase

Power source

A 3-phase power source which produces 3 phase voltages of equal rms value, but with $120°$ phase difference. $$

Phasor diagram

A graphical representation of the magnitude and phase relationship between different waveforms.

In a balanced 3-phase system, the phasor diagram shows three phasors (vectors) of equal length, separated by 120° angles. Each phasor represents the voltage of one phase. The diagram helps in visualizing the phase differences and the symmetry of the system.

Phase voltage

Voltage between a phase wire and the neutral wire.

$V_{\text{RN}}$, $V_{\text{YN}}$, $V_{\text{BN}}$ are the phase voltages.

Line-to-line voltage

Voltage between any 2 phase wires. Line-to-line voltages also have a $120°$ phase difference. $$

$V_{\text{RY}}$, $V_{\text{YB}}$, $V_{\text{BR}}$ are the line-to-line voltages or line voltages.

$$\big| V_{\text{BR}} \big| = 2 \times \big| V_{\text{BN}} \big| \cos(30°) = \sqrt{3} \big| V_{\text{BN}} \big|$$

Note

In a 3-phase system, line-to-line voltage is mentioned.

Analysis

$$I_N=E \bigg[ \frac{1\angle 0°}{z_R} + \frac{1\angle -120°}{z_Y} + \frac{1\angle 120°}{z_B} \bigg]$$

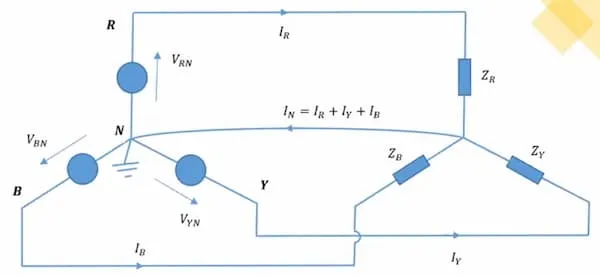
When the loads are balanced: $z_R=z_Y=z_B=z$, $I_N = 0$
In this case, neutral wire is optional and can be eliminated. $I_N=0$ have to be maintained so that the voltage is equal to ground voltage in neutral wire. This makes sure there are no power losses in neutral wire.

Real-life Usage

Most domestic loads are single-phase. In case of 3-phase domestic wiring, the single-phase loads are distributed among the 3 phases at the main distribution board.

Devices that have a 3-phase power input, doesn’t require a neutral line.

Per-phase Equivalent Circuit

Power, voltage, current, power factor are same for all $3$ phases. $$

When a 3-phase system is balanced, it is sufficient to consider only a single phase. The diagram showing the single-phase equivalent of the power system using standard symbols.

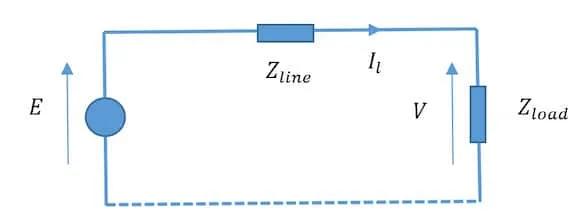
Here:

• $E$ - voltage across the source
• $V$ - voltage across the load

$$\text{Per-phase power} = |V_p||I_l|\cos\theta = \frac{1}{3}\times\text{3-phase power} \;\; \land \;\; |V_l|= \sqrt 3 |V_p|$$ $$\implies \text{3-phase power}= \sqrt{3}|V_l||I_l|\cos\theta$$

Here:

• $V_p$ - phase voltage
• $V_l$ - line voltage
• $I_l$ - line current
• $\cos\theta$ - power factor
• The power can either be source power, load power, or transmission power losses.

Unbalanced 3-phase system

A 3-phase system becomes unbalanced, when load distribution is not equal among the phases. $I_N\neq 0$. Highly undesirable. Neutral wire is the return path for the line currents and is compulsory. $$

Large currents in the neutral wire could cause:

• If neutral wire have significant impedance, different points of the neutral wire will have different voltage
• Series voltage unbalances can happen if the neutral wire is broken

Each phase will be different. Complete system has to be considered when analyzing the circuit.

Note

Analyis of unbalanced 3-phase systems is not required in s1.