Hydrostatic Pressure

At a point,

$$P = \lim_{\delta A \to 0} \frac{\delta F}{\delta A}$$

Pascal’s law

The hydrostatic pressure at a point is the same from all directions.

Proof

Consider the fluid element shown, containing the point $A$. $$

From the image: $\sin{\theta}=\frac{\Delta{z}}{\Delta{s}}\;\land\;\cos{\theta}=\frac{\Delta{x}}{\Delta{s}}$ $$

For equilibrium:

$$P_x(\Delta{y}\Delta{z})-P_s(\Delta{y}\Delta{s})\sin{\theta}=0 \implies P_x=P_s$$ $$P_z(\Delta{x}\Delta{y})-P_s(\Delta{y}\Delta{s})\cos{\theta}-\frac{1}{2}\Delta{x}\Delta{y}\Delta{z}\rho g=0 \implies P_z=P_s+\frac{1}{2}\Delta{z}\rho g$$

As all $\Delta{x},\Delta{y},\Delta{z}$ approaches $0$: $P_z=P_s$. Therefore $P_x=P_z=P_s$

Variation along directions

Proof

Let $p$ be the pressure at the point $A\equiv (x,y,z)$.

$$p = f(x,y,z)$$ $$dp = \frac{\partial p}{\partial x} \text{d}x + \frac{\partial p}{\partial y} \text{d}y + \frac{\partial p}{\partial z} \text{d}z$$

By considering equilibrium of this fluid element containing $A$. $$

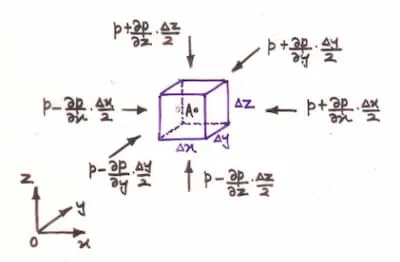
In the $x$ direction,$$

$$\bigg( p - \frac{\partial p}{\partial x} \frac{\Delta{x}}{2} \bigg) \Delta{y} \Delta{z} - \bigg( p + \frac{\partial p}{\partial x} \frac{\Delta{x}}{2} \bigg) \Delta{y} \Delta{z} = 0$$ $$\frac{\partial p}{\partial x} = 0$$

Similarly $\frac{\partial p}{\partial y} = 0$ can be proven. $$

In the $z$ direction,$$

$$\bigg( p - \frac{\partial p}{\partial z} \frac{\Delta{z}}{2} \bigg) \Delta{x} \Delta{y} - \bigg( p + \frac{\partial p}{\partial z} \frac{\Delta{z}}{2} \bigg) \Delta{x} \Delta{y} - \Delta{x} \Delta{y} \Delta{z} \rho g = 0$$ $$\frac{\partial p}{\partial z} = -\rho g$$ $$dp = -\rho g\,\text{d}z$$ $$p = -\int{\rho g\,\text{d}z}$$

For incompressible fluids

$\rho$ is constant. $$

$$p = -\rho g\int{\text{d}z} = -\rho gz + c = f(z)$$

Isobar

Surface of constant pressure.

Types of pressure

Atmospheric Pressure

Pressure exerted by atmospheric air.

Gauge Pressure

Measured in respect to atmospheric pressure.

Absolute Pressure

Measured in respect to perfect vaccum.

$$\text{Absolute Pressure} = \text{Atmospheric Pressure} + \text{Guage Pressure}$$

Piezometric pressure

$$P = -\rho gz + c$$ $$P + \rho gz = c = P^{*}$$

Pressure diagram

A diagram showing the variation of pressure along a submerged surface.

Pressure Head

Height of a particular fluid column that will produce the pressure at a point.

$$\text{Pressure head} = h = \frac{p}{\gamma}$$

Pressure difference between 2 points

Suppose there are 2 points $\text{A},\text{B}$ with a height difference of $h$.

$P_1 = -\rho gz_1 + c$

$P_2 = -\rho gz_2 + c$

$P_2 - P_1 = -\rho g(z_2 - z_1) = -\rho g (-h) = h \rho g$

$P_2 = P_1 + h \rho g$