Sahithyan's S1 — Fluid Mechanics

Hydrostatic Thrust

On a Plane Surface

Acts normal to the surface on the centre of pressure with a magnitude of:

\text{Thrust} = \text{submerged area} \times P_c

$C$ is the centroid of the submerged area. $P_c$ is the pressure at the centroid.

y_p = y_c + \frac{I_{\text{cc}}}{A\cdot y_c}

Here:

$A$ - Total submerged area
$y_p$ - Distance to centre of pressure measured along the submerged surface from the free surface
$y_c$ - Distance to $C$ measured along the submerged surface from the free surface
$I_{\text{cc}}$ - Second moment of submerged area about the centroidal axis parallel to the free surface

Shape	Description	$y_p$
Parallelogram	Base $b$ . Height $h$ . Base is at the free surface.	$\cfrac{2h}{3}$
Triangle	Base $b$ . Height $h$ . Base is at the free surface.	$\cfrac{5h}{6}$
Circle	Radius $r$ . Center is at a depth $r$ .	$\cfrac{5r}{4}$

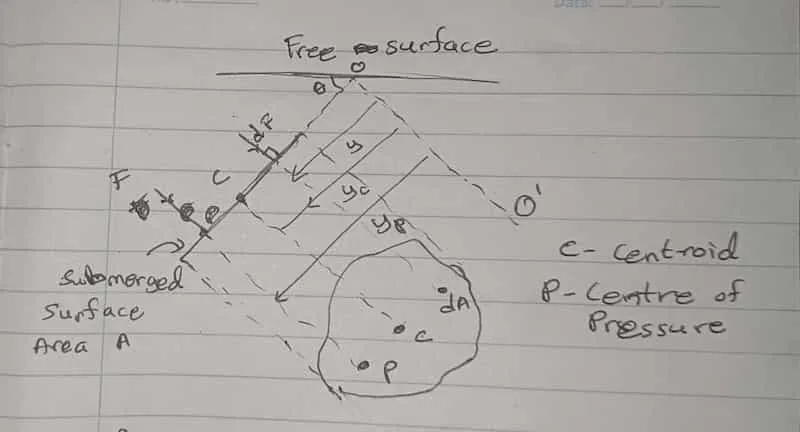
Hydrostatic thrust on a plane surface

All forces acting on the surface is normal to the surface. Therefore $F$ is normal to the surface.

F = \int_A{\text{d}F} = \int_A{p\text{d}A} = \int_A{y\sin{\theta}\rho g\, \text{d}A}

F = \sin{\theta}\rho g \int_A{y\,\text{d}A} = \sin{\theta}\rho g \cdot A y_{c} = A\cdot {y_{c}\sin{\theta}\rho g}

F = AP_c

F \cdot y_p = \int_{A}{y\,\text{d}F}

y_p = \frac{\int_{A}{y\,\text{d}F}}{\int_{A}{\text{d}F}} = \frac{\int_{A}{y(y\sin{\theta}\rho g)\,\text{d}A}}{\int_{A}{y\sin{\theta}\rho g\,\text{d}A}} = \frac{\int_{A}{y^2\,\text{d}A}}{\int_{A}{y\,\text{d}A}}

y_p = \frac{I_{oo}}{Ay_c} = y_c + \frac{I_{cc}}{Ay_c}

F_x = \text{Thrust exerted on the vertical projection of the submerged surface}

F_y = \text{Weight of the fluid above submerged surface}

Hydrostatic thrust on a curved surface

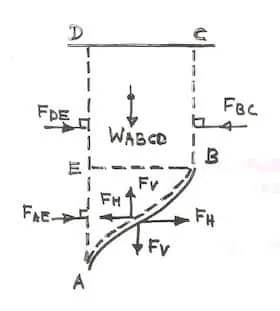
For the equilibrium of the fluid volume $ABCDA$ .

F_y = W_{ABCDA}

For the equilibrium of the fluid volume $ABEA$ .

F_x = F_{AE}