Relative Equilibrium

When a fluid-contained vessel moves with a constant acceleration it will be transmitted to the fluid. The fluid particles will move to a new position and remain in such position in equilibrium, relative to the vessel. Such equilibrium is known as the Relative Equilibrium of a fluid.

Under linear acceleration

No flow of the fluid (relative to the fluid particles). No shear forces, and all forces are normal to the surface they act on. Hence, fluid statics equations can be used in relative equilibrium.

Variation of pressure

Let .

Consider the fluid element containing point which is under an acceleration of in the directions.

By applying Newton’s second law of motion in all 3 directions:

Substituting all the terms:

Integrating both sides:

Shape of free surface

On the free surface as gauge pressure is considered.

Free surface is a plane in 3D.

Inclination from horizontal plane

The free surface has an inclination from the horizontal plane: , the slopes in and directions.

To find , it is possible to set since movement in the direction does not affect the slope in the direction. A point can move along the surface in the -plane by choosing any fixed value. After setting , the free surface equation is differentiated with respect to :

Similarily can be solved:

Horizontal Acceleration

Equation of the free surface

Is a straight line in axes. The straight line is at an inclination of :

Vertical Pressure Distribution

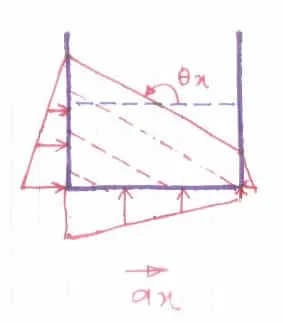
Vertical Acceleration

Equation of the free surface

Horizontal straight line.

Vertical Pressure Distribution

Here:

• - hydrostatic pressure
• - due to

Varies only in direction. Increases with height. Isobars are horizontal.