Deviations from the ideal in real trusses.
- Loads are not applied only at joints; hence there is bending in members
- Joints are not perfectly pinned, so moments can be developed at joints
Method of Joints
Section titled “Method of Joints”Principle
Section titled “Principle”Since the truss is in equilibrium, each pin joint must also be in equilibrium.
Sign convention
Section titled “Sign convention”Forces acting on each joint is marked. Tensile forces are positive. Compressive forces are negative.
Method
Section titled “Method”- Find external reactions using equilibrium equations for the entire truss.
- Start with a joint with only 2 unknown joint forces.
- Mark the forces (consider all forces are tensile) acting on the joint.
- Find the unknown forces at the selected joint, using 2 equilibrium equations for the joint.
- Go to all other joints in turn and find forces in all the members.
Special cases
Section titled “Special cases”| Case | Description |
|---|---|
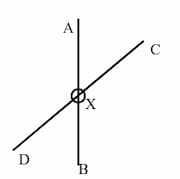 | |
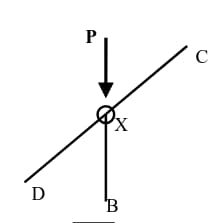 | |
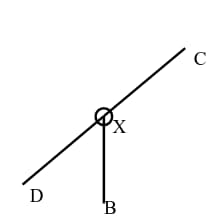 | |
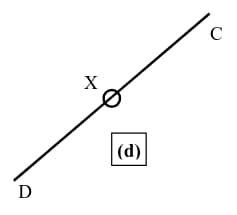 | |
 |
Method of Sections
Section titled “Method of Sections”Principle
Section titled “Principle”Since the truss is in equilibrium, each of its section must be in stable equilibrium.
Method
Section titled “Method”- Decide on which member’s internal force must be calculated.
- Cut the truss through 3 or less members including the target member.
- Internal forces in cut members become external forces. Can be represented as tensile forces.
- Use equilibrium equations for RHS or LHS section to find the internal forces.