Beams

• long ()
• axis of the beam is straight
• constant cross-section throughout its length

Classified by supporting conditions

First 3 are the mandatory ones in s1.

u.d.l means uniformly distributed load.

Type	Image	Notes
Simply supported beam		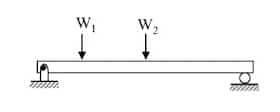At ends: Max SF and BM = 0
Cantilevered beam		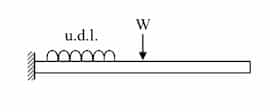At fixed end: Max SF and BM
Overhanging beam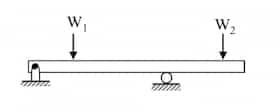
Propped cantilevered beam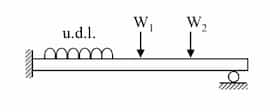
Continuous beam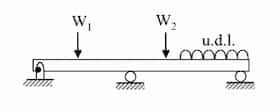
Fixed beam		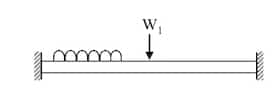At ends: Max SF and BM

At a section

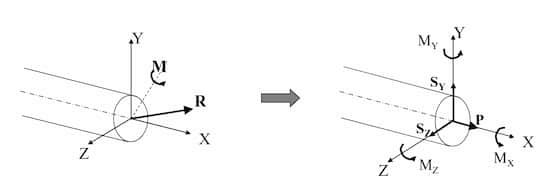
• - Normal force / Axial force
• - Shear forces along and axis
• - Twisting moment / Torque
• - Bending moments about and axis

Degress of freedom

A plane member have 3 degrees of freedom. Any of the 3 can be restrained.

• Displacement in -direction
• Displacement in -direction
• Rotation about -direction

SFD & BMD

Sign convention

• Bending moment
  • Hogging (curves upwards in the middle) is (+) ve
  • Sagging (curves downwards in the middle) is (-) ve
• Shear force
  • Clockwise shear is (+) ve.
  • Counterclockwise shear is (-) ve.

Pure bending

A member is in pure bending when shear force is and bending moment is a constant.

Point of Contraflexure

The point about which bending moment is , and changes its sign through the point.

Distributed load

Suppose a beam is under a distributed load of per unit length.

Deflection of a beam

Suppose a simply supported beam is applied a load of at mid-span.

Here:

• - Maximum stress
• - Deflection
• - Load
• - Span length
• - Young’s modulus
• - Second moment of cross-sectional area

Principle of Superposition

A beam with multiple loads can be split into multiple systems each with a single load. Reason for doing so is the ease of calculations.

Values will be the sum of each system’s corresponding value.