Miller Indices

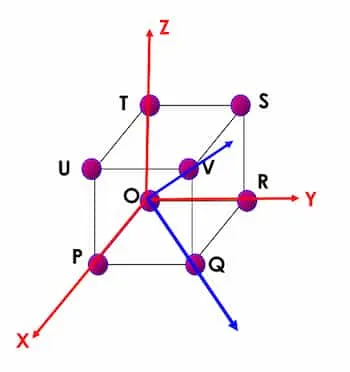
Any vertex can be chosen as the origin.

Notation

• Minus noted with a bar
• Addition and subtraction is carried out like vectors
• - Atom/Vertex
• - Direction, no commas
• - Family of directions
• - Plane, no commas
• - Family of planes
• Always will be whole numbers. Fractions must be multiplied by LCM.

Direction

Equivalent directions are grouped into a family.

Direction families

<100>

• No of planes:

<110>

• No of planes:

<111>

• No of planes:

The above are the common directions. There are other directions as well.

Show the direction

To show the direction , for example:

Take the point . Divide by the highest number (, in this case) to bring the point inside the unit cell. The resulting point will be . The direction is given by vector from to the resulting point.

Close packed direction

All neighbour atoms in a direction touch each other. For example: of fcc.

Plane

Steps

• If sitting on any axes, move the origin.
• Find the intercepts. if parallel.
• Find the reciprocals.

Plane families

100

• Denotes as
• No of planes:

110

• Denotes as
• No of planes:

111

• Denotes as
• No of planes:

The above are the common planes. There are other planes as well.

Show the plane

• Divide by the smallest non-zero number.
• Find the reciprocals. means parallel to the axis.

Close packed plane

All neighbour atoms in a crystal plane touch each other. For example: of fcc.

Planar Density / Aerial Density

Number of atoms in a unit area in a specific plane. Differs between different planes in a single crystal structure.