Carbon Nanotubes

A rolled up sheet of graphene.

Classifications

Based on structure

1. Single wall carbon nanotubes (SWNT)
2. Multi-walled carbon nanotubes (MWNT)
   Similar to graphite but rolled up as a set of sheets.

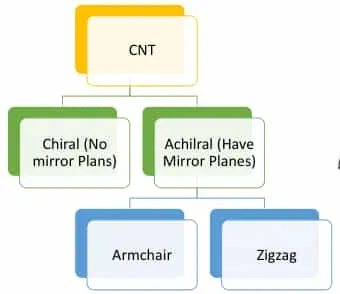
Based on Chirality

Chirality means the way that graphene sheet is oriented with respect to the axis of carbon nanotube.

Achiral

Have mirror planes. Has 2 types.

1. Armchair
2. Zigzag

Armchair

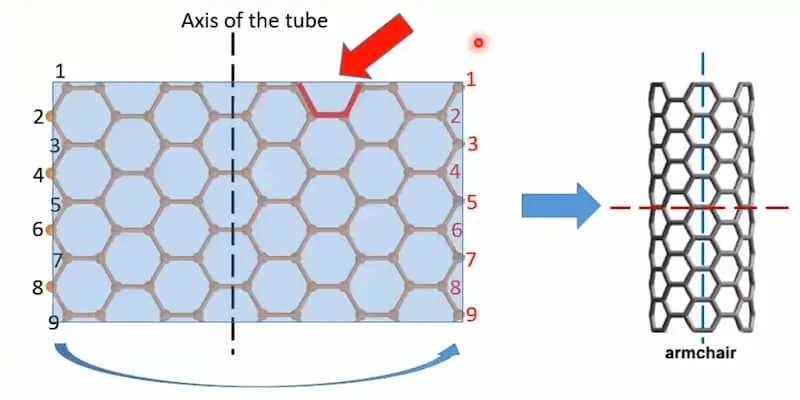
Circumference has a repeating armchair structure.

Zigzag

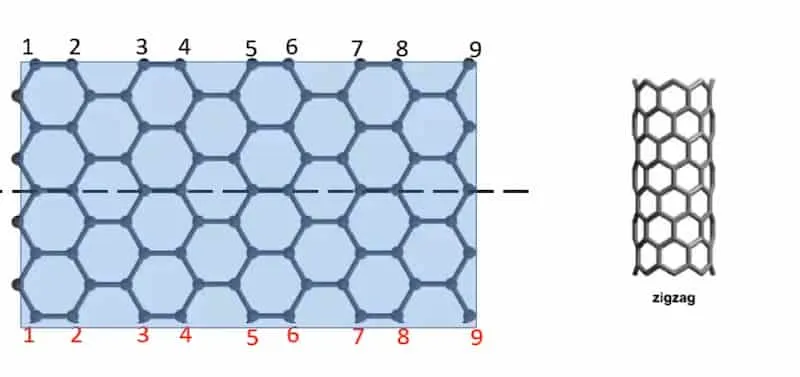
Circumference has a repeating zigzag structure.

Chiral

No mirror planes. Definition for the chiral type is later explained.

Definitions

Equivalent Atoms

Equivalent atoms means the atoms having the same surrounding.

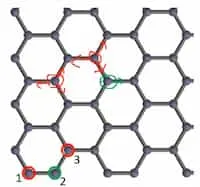
In graphene, next-near neighbours are equivalent atoms.

When a graphene sheet is rolled to create a CNT, only equivalent atoms can be connected.

Primitive Vectors

Vectors used to describe a unit cell.

For graphene, any 2 adjacent sides of the unit cell can be used as the primitive vectors.

Lattice Vectors

Any vector connecting 2 equivalent atoms. A lattice vector can be expressed in terms of primitive vectors.

Chiral Vector

The vector that constructs the circumference of a CNT. Also called as Circumferential vector.

(n,m) notation

If the chiral vector can be expressed as $na_1 + ma_2$ where $a_1,a_2$ are the primitive vectors, then the notation for the nanotube is $(n,m)$

• $n=0 \lor m =0$: zigzag tube
• $n=m$: armchair tube
• Otherwise: chiral tube

Chiral Angle

Angle between the chiral vector and nearest zigzag angle.

For a $(n,m)$ tube where $n>0$ and $n\ge m\ge 0$:

$$\theta=\tan^{-1}\bigg( \frac{\sqrt{3}m}{2n+m}\bigg)$$

• $\theta=30°$: armchair tube
• $\theta=0°$: zigzag tube
• $0°<\theta<30°$: chiral tube

Chiral Vector Length

For a $(n,m)$ tube, the chiral vector’s length is given by: $$

$$|\text{CH}|=a\sqrt{n^2+m^2+nm}$$

Here $a$ is the bond length of C-C. $$

Diameter of CNT

The diameter can be expressed by:

$$D=\frac{|\text{CH}|}{\pi}=\frac{a}{\pi}\sqrt{n^2+m^2+nm}$$

Properties

• Mechanical properties
  • High young’s modulus
    Depends on tube diameter, multi-walled or single-walled but not tube chirality. Multi-walled CNTs have higher young’s modulus.
  • Sustains higher strain
• Electrical properties
  • Depends on chirality and size
  • Exhibits superconductivity at $20\text{K}$
  • Band structure changes with chirality
• Thermal properties
  • Conducts thermal energy only in the axial direction; radial direction is insulating

Chirality-dependent

For a $(n,m)$ tube: $$

• If $n=m$, its armchair typed and is metallic (good conductors)
• If $n-m$ is a integer multiple of $3$: small band gap semiconductors
• Else: large band gap semiconductors

Band gap decreases as the radius increases.

Applications

• Conductive or reinforced plastic
• CNT based transistors
• Molecular electronics
• Energy storage devices
• Biomedical applications